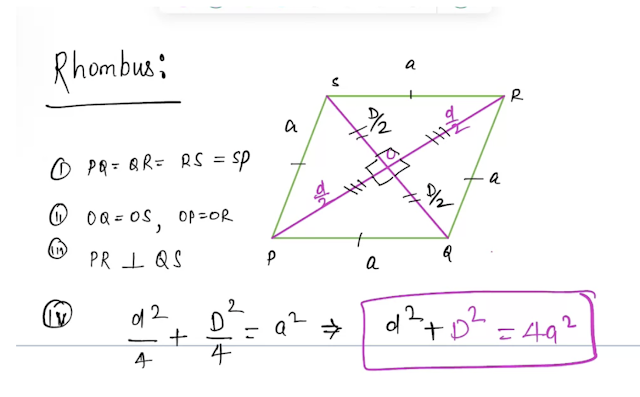
More about quadrilaterals

 Rectangle properties:




























Problems: Prove that medians/altitudes/angle bisectors of a triangle are concurrent.
For altitudes:












Solution:
If you apply the formula for CosA and CosC this problem is effectively to prove that c.CosA = b.CosC.
but c.CosA = AH
So pr. that AH = b.CosC
but CosC = CH/a
So pr. that. AH/CH = b/a
By Angle Bisector theorem b/a = AD/BD.
So pr. that AH/CH = AD/BD.
By Ceva's theorem AD/BD * BM/CM * CH/AH = 1
But BM = CM
So AD/BD = AH/CH
Hence proved.





















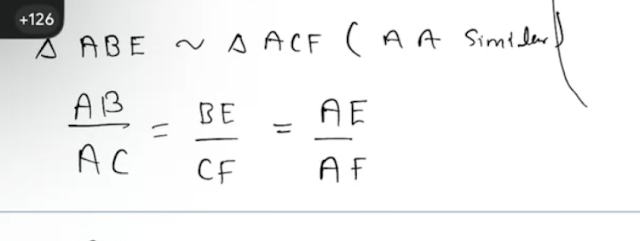
Comments

Post a Comment

Popular posts from this blog

Combinatorics DPP - RACE 6 - Q16 pending discussion

Image
Q1 . A question paper consists of two sections. Section A has 7 questions and section B has 8 questions. A student has to answer 10 questions out of these 15 questions. The number of ways in which he can answer if he must answer at least 3 of section A and at least 4 of the section B is: Solution: One wrong way to solve this: For the mandatory questions: 7C3*8C4 Now 3 more questions need to be answered from 4 of A and 4 of B. Cases: 3A,0B | 2A,1B | 1A,2B | 0A,3B 4C3*4C0 + 4C2*4C1 + 4C1*4C2 + 4C0*4C1 = 4 + 24 + 24 + 4 = 56 Finally: 7C3*8C4*56 = 35*70*56 = 137200 Why is it wrong? Let's say we chose A1,A2,A3 as mandatory from A and then chose A4,A5,A6 when we did 4C3*4C0 for (3A,0B). But we could have done it the other way round also, i.e. choose A4,A5,A6 as mandatory and then choose A1,A2,A3. So there is overcounting. Correct Solution : Simply create the cases for A,B: (3,7),(4,6),(5,5),(6,4) 7C3*8C7 + 7C4*8C6 + 7C5*8C5 + 7C6*8C4 = 2926. Q2 . A kindergarten teacher has 25 kids in her...
Read more

Geometry practice problems

Image
Solutions: Q1: sqrt(56)/4 Q2: 3 Q3: 25/2 Q4: sqrt(3) - 1 Q5: 2 Q6: 14 Q7: 208 A1B1C1D1 is a parallelogram by applying midpoint theorem multiple times.  A1B1 || AC and B1C1 || BD. Also A1B1  = AC/2 and B1C1 = BD/2. Again by MP theorem diagonals of A1B1C1D1 are 8 and 12 and also perpendicular to each other. If diagonals of a parallelogram are perpendicular to each other, it's a rhombus. So A1B1C1D1 is a rhombus. With all sides equal. A1B1 = B1C1 so AC = BD so it's enough to find one diagonal. In the rhombus A1B1C1D1, taken one quarter formed by its diagonals and find one side. A1B1 = sqrt(16 + 36) = sqrt(52) AC = 2sqrt(52) = sqrt(208) AC.BD = 208 Q8: 36 [BXCY] = 13k [ABC] = 18k = 6AC => AC = 3k [AXY] = 18k - 13k = 5k AXY ~= BXY by SAS So [BXY] = 5k [BCY] = 18k - 5k - 5k = 8k = 6.CY => CY = 4k/3 AY = AC - CY = 5k/3 = BY by congruence earlier. In triangle BCY, BY^2 = 12^2 + CY^2= 144+(4k/3)^2 = (5k/3)^2 => 144 = k^2 => k = 12 => AC = 12.3 = 36 Q9: 49 Sides are 8,24,...
Read more

Pre RMO 2018(IOQM), Question 2 incircle quadrilateral

Question 2, Pre RMO 2018-19(IOQM): In a quadrilateral ABCD, it is given that AB = AD = 13, BC= CD = 20, BD = 24. If r is the radius of the circle inscribable in the quadrilateral, then what is the integer closest to r?. Prerequisites: 1. Incenter, incircle and angle bisectors in triangle/polygons 2. Kite diagonals Solution : ABCD is a kite. So, A C ⊥ B D AC \perp BD . So, B O = O D = 12  cm BO = OD = 12 \text{ cm} . A O = 13 2 − 12 2 = 5  cm AO = \sqrt{13^2 - 12^2} = 5 \text{ cm} O C = 20 2 − 12 2 = 16  cm OC = \sqrt{20^2 - 12^2} = 16 \text{ cm} ar ( □ A B C D ) = 1 2 × A C × B D \text{ar}(\square ABCD) = \tfrac{1}{2} \times AC \times BD = 1 2 × 21 × 24 = \tfrac{1}{2} \times 21 \times 24 = 252  cm 2 = 252 \text{ cm}^2 r = Δ S = 252 33 = 7.63  cm r = \frac{\Delta}{S} = \frac{252}{33} = 7.63 \text{ cm} Closest integer = 8 = 8 .
Read more